Microsoft Excel'de Çan Eğrisi Grafiği Nasıl Oluşturulur

Grafikler ve Excel grafikleri, karmaşık veri kümelerini görselleştirmenin harika bir yoludur ve Çan eğrileri de istisna değildir. Normal bir dağılımı kolayca analiz etmenize olanak tanırlar ve Excel'de kolayca oluşturulabilirler. Şimdi bunun nasıl olduğunu öğrenelim.

Çan eğrisinin amacının yalnızca verileri güzelleştirmenin ötesine geçtiğini unutmayın. Böyle bir grafik üzerinde gerçekleştirilebilecek, veri kümesinin birçok eğilimini ve özelliğini ortaya çıkarabilecek birçok veri analizi biçimi vardır. Ancak bu kılavuzda çan eğrisini analiz etmeye değil, yalnızca oluşturmaya odaklanacağız.

Normal Dağılıma Giriş

Çan eğrileri yalnızca normal şekilde dağıtılan veri kümelerini görselleştirmek için kullanışlıdır. Çan eğrilerine dalmadan önce normal dağılımın ne anlama geldiğine bir göz atalım.

Temel olarak, değerlerin büyük ölçüde ortalama etrafında kümelendiği herhangi bir veri kümesine normal dağılım (veya bazen adlandırıldığı şekliyle Gauss dağılımı) adı verilebilir. Çalışan performans sayılarından haftalık satış rakamlarına kadar doğal olarak toplanan veri kümelerinin çoğu bu şekildedir.

Çan Eğrisi Nedir ve Neden Yararlıdır?

Normal dağılımdaki veri noktaları ortalama etrafında kümelendiğinden, her veri noktasının mutlak değerinden ziyade merkezi ortalamadan varyansını ölçmek daha kullanışlıdır. Ve bu varyansların bir grafik biçiminde çizilmesi bir Çan Eğrisi verir.

Bu, aykırı değerleri bir bakışta tespit etmenize ve veri noktalarının ortalamaya göre göreceli performansını görmenize olanak tanır. Çalışan değerlendirmeleri ve öğrenci puanları gibi konularda bu, düşük performans gösterenleri ayırt etme olanağı sağlar.

Çan Eğrisi Nasıl Oluşturulur

Birçok Excel'deki basit grafikler 'in aksine, veri kümenizde yalnızca bir sihirbaz çalıştırarak çan eğrisi oluşturamazsınız. Verilerin öncelikle biraz ön işleme ihtiyacı vardır. Yapmanız gerekenler şöyle:

Verileri artan düzende sıralayarak başlayın. Sütunun tamamını seçip ardından Veri>Artan Düzende Sırala'ya giderek bunu kolayca yapabilirsiniz.

Sonra, Ortalamaişlevini kullanarak ortalama değeri (veya Ortalamayı) hesaplayın. Sonuç genellikle ondalık sayılarda olduğundan, bunu Yuvarlakişleviyle de eşleştirmek iyi bir fikirdir.
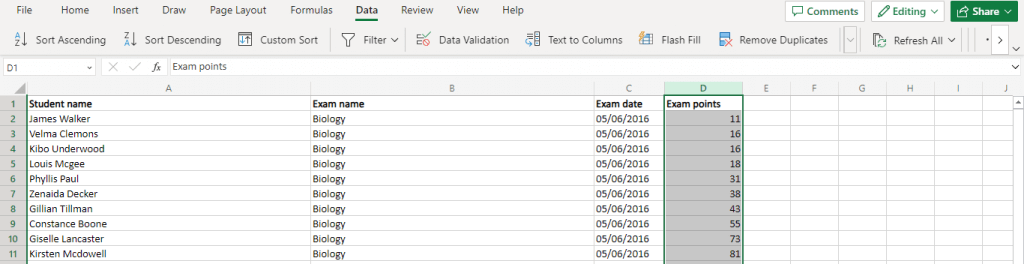
Örnek veri kümemiz için, işlev şuna benzer:
=YUVARLAK (ORTALAMA(D2:D11),0).

Artık Standart Sapmayı hesaplamak için iki fonksiyonumuz var. STDEV.S, popülasyonun yalnızca bir örneğine sahip olduğunuzda (genellikle istatistiksel araştırmalarda) kullanılırken, STDEV.P, veri kümesinin tamamına sahip olduğunuzda kullanılır.

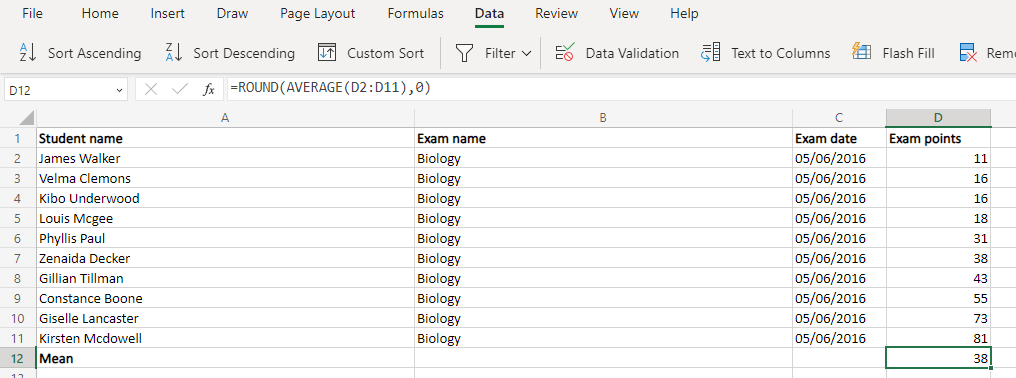
Gerçek hayattaki uygulamaların çoğu için (çalışan değerlendirmesi, öğrenci notları vb.) STDEV.P idealdir. Bir kez daha, bir tam sayı elde etmek için Yuvarlama işlevini kullanabilirsiniz.

=YUVARLA(STDEV.P(D2:D11),0)

Tüm bunlar ihtiyacımız olan gerçek değerlere, yani Normal dağılıma yönelik hazırlık çalışmasıydı. Elbette Excel'in bunun için de özel bir işlevi zaten var.

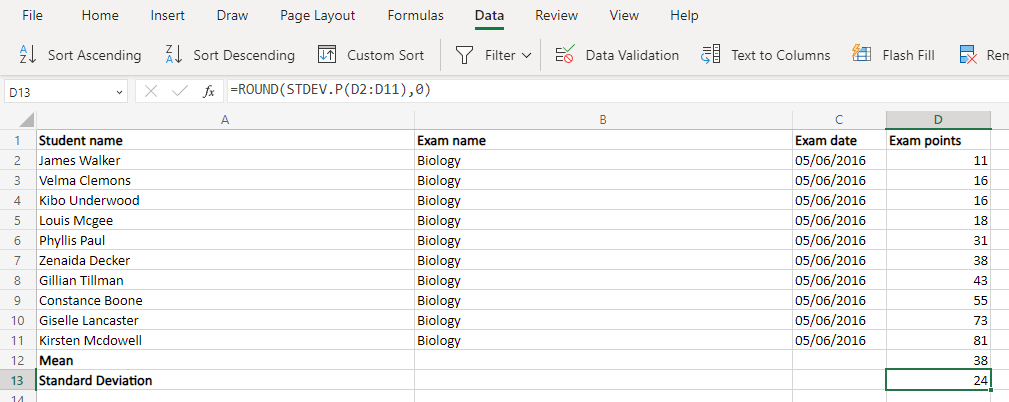
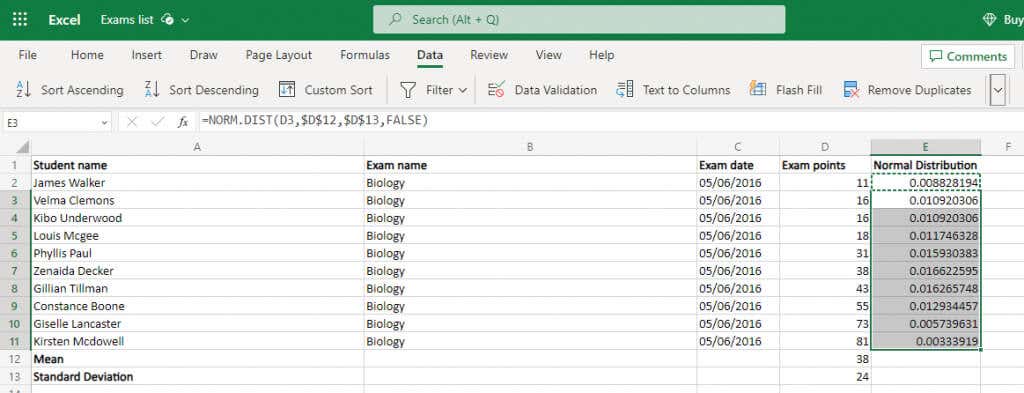
NORM.DAĞişlevi dört bağımsız değişken alır: veri noktası, ortalama, standart sapma ve bir Kümülatif dağıtımı etkinleştirmek için boole bayrağı. Sonuncuyu güvenle göz ardı edebiliriz (FALSE yazarak) ve zaten ortalamayı ve sapmayı hesapladık. Bu, yalnızca hücre değerlerini girmemiz gerektiği ve sonucu elde edeceğimiz anlamına gelir.

=NORM.DAĞ(D2,$D$12,$D$13,FALSE)

Şunun için yapın: bir hücre ve ardından formülü tüm sütuna kopyalayın; Excel, yeni konumlarla eşleşecek şekilde referansları otomatik olarak değiştirecektir. Ancak öncelikle $ sembolünü kullanarak ortalama ve standart sapma hücre referanslarını kilitlediğinizden emin olun.

Orijinal değerlerle birlikte bu normal dağılımı seçin. Orijinal veri noktaları x eksenini oluştururken dağılım y eksenini oluşturacaktır.

Eklemenüsüne gidin ve dağılım diyagramlarına gidin. Düz Çizgilerle Dağılımseçeneğini seçin.

MS Excel'de Çan Eğrisi Grafiği Oluşturmanın En İyi Yolu Nedir?

Çan eğrisi grafikleri karmaşık görünebilir ancak oluşturulması aslında oldukça basittir. İhtiyacınız olan tek şey, veri kümenizin normal dağılım noktalarıdır.

Öncelikle yerleşik Excel formüllerini kullanarak ortalamayı ve standart sapmayı belirleyin. Daha sonra tüm veri kümesinin normal dağılımını hesaplamak için bu değerleri kullanın.

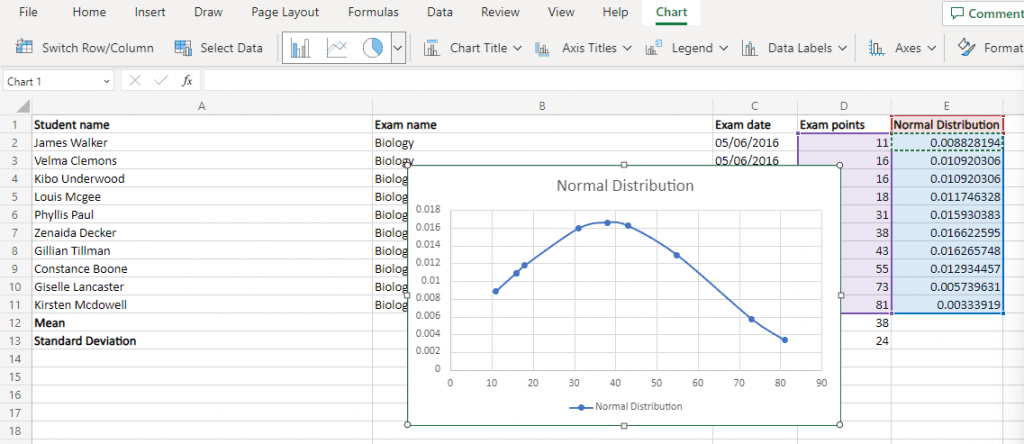
Çan eğrisi grafiği, yalnızca x ekseni için orijinal veri noktalarını ve y ekseni için normal dağılım değerlerini kullanan bir Düz Çizgili Dağılımgrafiğidir. Veri kümeniz normal şekilde dağılmışsa Excel'de düzgün bir çan eğrisi elde edersiniz.

Artık Excel'de çan eğrisi grafiğinin nasıl oluşturulacağını bildiğinize göre, uygulamanız için Gantt şeması oluştur, sıcaklık haritası veya şelale grafiği 'in nasıl oluşturulacağına bakın. sıradaki proje.

.

İlgili Mesajlar: